这篇文章是SICP一书中第二章的笔记。
文章中用到的图来源Sarabander.github.io/SICP
例子中的;后的内容表示输出。
Scheme语法简述
1 ;数值
(+ 1 1) ;表达式,+为操作符,1 1为操作数
(define a 2) ;定义变量
(define (f i)
(+ i 1)) ;定义过程
(define f
(lambda (i)
(+ i 1))) ;定义过程 -- 将f与lambda表达式关联
(if (> a 1)
a
1) ;条件结构
(cond ((= a 1) 1)
((> a 1) a)
(else 2)) ;条件结构
数据抽象导论
数据抽象的基本概念就是构造一个在“抽象数据”上操作的程序,也就是说它是在用复合数据对象。
考虑如何表示有理数?每个有理数都可以由一个实部和一个虚部组成,所以一个“有理数对象”应该包含了两个原始数据。
,
,
,
,
当且仅当 .
我们先假设已经有了numer,denom和make-rat三个过程,它们的作用分别是取出分子,取出分母和通过分子和分母构造一个新的有理数对象。
(define (add-rat x y)
(make-rat (+ (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (sub-rat x y)
(make-rat (- (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (mul-rat x y)
(make-rat (* (numer x) (numer y))
(* (denom x) (denom y))))
(define (div-rat x y)
(make-rat (* (numer x) (denom y))
(* (denom x) (numer y))))
(define (equal-rat? x y)
(= (* (numer x) (denom y))
(* (numer y) (denom x))))
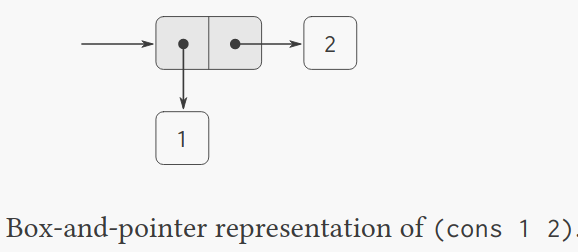
为了让我们能够实现数据抽象,我们的语言为我们提供了一个复合结构,叫做Pair。
看个简单的例子
(define x (cons 1 2))
(car x) ;1
(cdr x) ;2
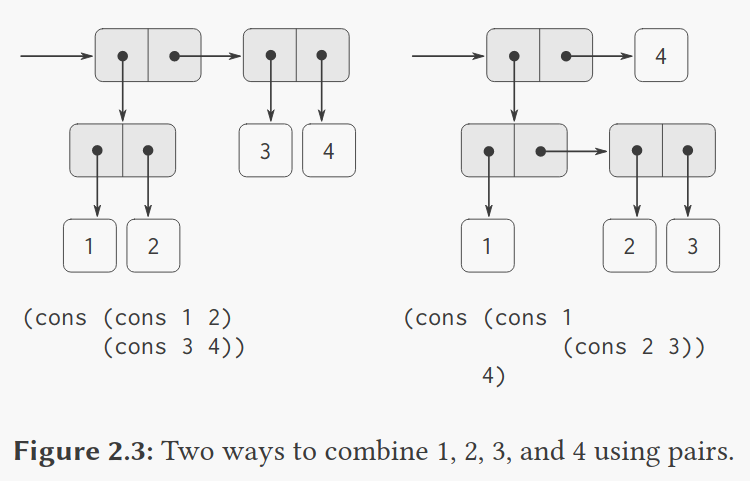
事实上,cons更多地被用来组合那种自身就是由Pair组成的的Pair。
(define x (cons 1 2))
(define y (cons 3 4))
(define z (cons x y))
(car (car z)) ;1
(car (cdr z)) ;3
那么,现在我们可以利用这三个过程来实现之前用到的make-rat,numer和denom了。
(define (make-rat n d) (cons n d))
(define (numer x) (car x))
(define (denom x) (cdr x))
抽象屏障

像这样,不同的过程将使用者和其底层实现分开的,这样的过程即是上一层的实现,也是下一层的接口,同时其定义了抽象屏障并连接了不同的层级。
什么是数据
数据是什么,之前我们并没有直接定义数据,而是通过定义构造过程和选择过程来描述该数据可支持的行为。
层次性数据和闭包性质
表示序列
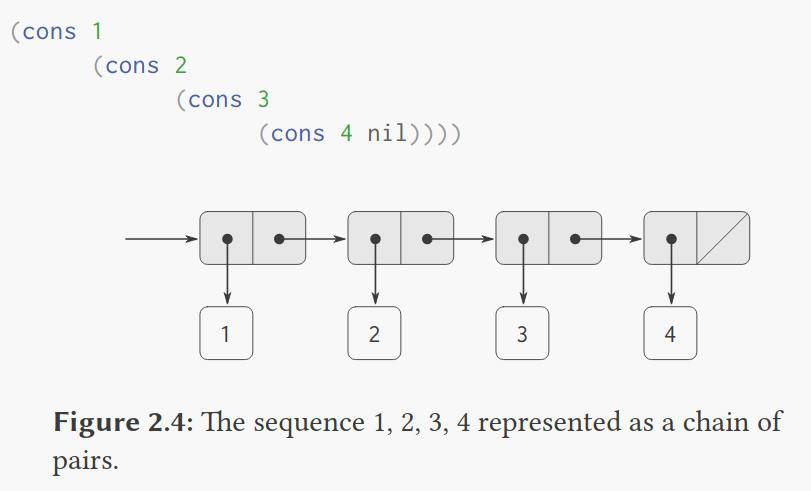
序列是很常用的结构,我们可以通过嵌套调用cons来实现。
对应的,我们需要一些对列表进行操作的过程。
考虑list-ref的定义:
- For n=0, list-ref should return the car of the list.
Otherwise, list-ref should return the (n−1)-st item of the cdr of the list.
(define (list-ref items n)
(if (= n 0)(car items) (list-ref (cdr items) (- n 1))))(define squares
(list 1 4 9 16 25))(list-ref squares 3) ;16
类似地,我们定义一个length过程,其接收一个列表作为参数,返回该列表的长度。
(define (length items)
(if (null? items)
0
(+ 1 (length (cdr items)))))
(define odds
(list 1 3 5 7))
(length odds) ;4
(define (scale-list items factor)
(if (null? items)
nil
(cons (* (car items) factor)
(scale-list (cdr items)
factor))))
(scale-list (list 1 2 3 4 5) 10) ;(10 20 30 40 50)
你能看出这个过程实现了什么功能吗?
(define (map proc items)
(if (null? items)
nil
(cons (proc (car items))
(map proc (cdr items)))))
(map abs (list -10 2.5 -11.6 17)) ;(10 2.5 11.6 17)
(map (lambda (x) (* x x)) (list 1 2 3 4)) ;(1 4 9 16)
(define (scale-list items factor)
(map (lambda (x) (* x factor))
items))
我们可以抽象出一个map过程,它接收一个过程proc和一个序列items,其逐一将proc应用于items中的元素,并返回新的序列。
层次性结构

从另一个角度来看,我们可以把这些元素为序列的序列看作是一棵树。正如树有分支,可以称之为子树,而子树也可以有子树一般。
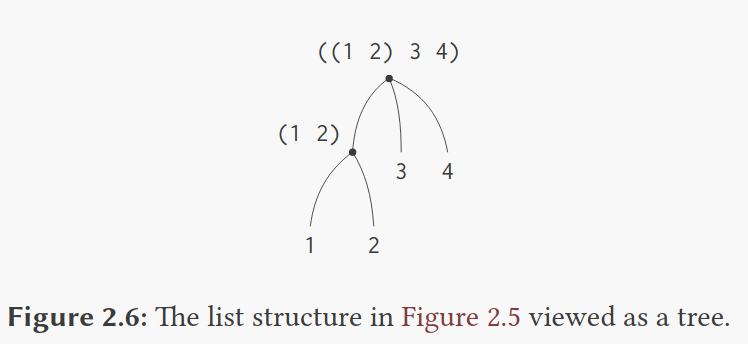
用递归来处理树结构再合适不过了。
我们可以将对树的操作规约到对其分支的操作,而这个操作又可以规约到对其分支的分支的操作,如此直至规约到对叶子节点的操作。
来比较一下序列操作和树操作:
(define x (cons (list 1 2) (list 3 4)))
(length x) ;3
(count-leaves x) ;4
(list x x) ;(((1 2) 3 4) ((1 2) 3 4))
(length (list x x)) ;2
(count-leaves (list x x)) ;8
回忆一下,之前对序列求长度的过程length是如何利用递归实现的。
- Length of a list x is 1 plus length of the cdr of x.
- Length of the empty list is 0.
count-leaves是类似的。空序列的返回值是0。
但到了规约阶段时,当我们利用car从列表中取值时,我们必须考虑这个值–它自己也可能是个树。
因此,合适的规约步骤如下:
Count-leaves of a tree x is count-leaves of the car of x plus count-leaves of the cdr of x.
最后,随着car的多次调用,我们最终规约至实际的树叶,所以我们需要对这个基本情况做处理:
Count-leaves of a leaf is 1.
为了方便我们写针对树的递归过程,Lisp提供了一个原始谓词过程pair?,它会测试其参数是否是一个序对。
完整的过程实现如下:
(define (count-leaves x)
(cond ((null? x) 0)
((not (pair? x)) 1)
(else (+ (count-leaves (car x))
(count-leaves (cdr x))))))
正如map处理序列时是一个很有力的抽象,使用map和递归一同处理树也是很方便的。
scale-tree将树中每个叶子节点按照对应的比例缩放。
(define (scale-tree tree factor)
(cond ((null? tree) nil)
((not (pair? tree))
(* tree factor))
(else
(cons (scale-tree (car tree)
factor)
(scale-tree (cdr tree)
factor)))))
(scale-tree (list 1
(list 2 (list 3 4) 5)
(list 6 7))
10)
;(10 (20 (30 40) 50) (60 70))
另一种实现方式就是将树当做一个子树的序列,这样我们就可以用上map过程(map是针对序列的)。
(define (scale-tree tree factor)
(map (lambda (sub-tree)
(if (pair? sub-tree)
(scale-tree sub-tree factor)
(* sub-tree factor)))
tree))
序列作为一般化的接口
前面使用复合数据时,我们已经充分了解了数据抽象给我们带来的好处,数据抽象让我们得以保留与另一种实现工作的灵活性而又不至于陷入数据表示的细节。
在这一小节,我们介绍另一种在使用复合数据时很有用的设计原则————那就是一般化接口的使用。
在1.3节中我们看见了程序抽象是如何实现为高阶过程的,高阶过程可以捕获程序中处理数字数据的通用模式。
在处理复合结构时,我们做类似运算的能力很大程度上取决于我们如何使用数据结构。
考虑下面类似于count-leaves的过程,这个过程接收一个树作为参数,如果叶子节点的值是奇数,就求其平方并累加。
(define (sum-odd-squares tree)
(cond ((null? tree) 0)
((not (pair? tree))
(if (odd? tree) (square tree) 0))
(else (+ (sum-odd-squares
(car tree))
(sum-odd-squares
(cdr tree))))))
这个过程和下面的过程看起来很不一样,even-fibs构造一个列表,如果Fibonacci序列中对应索引为n的数是偶数(其中n<=k),则将其加入列表。
(define (even-fibs n)
(define (next k)
(if (> k n)
nil
(let ((f (fib k)))
(if (even? f)
(cons f (next (+ k 1)))
(next (+ k 1))))))
(next 0))
尽管这两个过程结构上有很大的不同,但如果我们观察这两个过程的更加抽象的描述,我们就会发现这两个运算其实是十分相似的。
第一个程序:
- 枚举树的叶子
- 过滤它们,只选取值为奇数的叶子
- 对选取的叶子的值求平方,然后
- 使用+将其累加到结果上,初始值为0
第二个程序:
- 枚举从0到n的所有整数
- 以每个整数作为索引,求其对应到Fibonacci序列中的数
- 过滤它们,只选取值为偶数的数,然后
- 使用cons将其累加到结果上,初始值为空列表
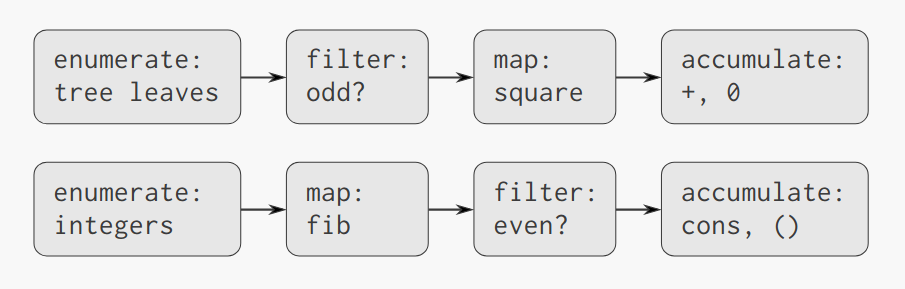
在sum-odd-squares中,首先由枚举器开始,它生成一个由给定树的叶子构成的“信号”。这个信号被传给过滤器,它将除了奇数以外的所有数字移除。
之后信号被传递至映射器,它是一个“变频器”,它将square这个过程应用于每个元素。映射器的结果传递给了累加器,它将元素用+混合,累加的初始值是0。
类似的,在even-fibs中也是如此。
不幸的是,以上的两个过程定义并没能把这样的信号流结构展示出来。
以上描述的enumerate,filter,map和accumulate的定义被混杂在这两个过程定义之中,如果我们能够重新整理程序,使得信号流结构得以体现在我们写的过程中,最终我们就可以得到概念更清晰的代码。
序列操作
重新组织程序以更清楚地反映出信号流结构的关键就是–关注在过程中一个阶段到下一个阶段中流动的“信号”。
如果我们将这些信号用序列来表示,那么我们就可以使用序列操作来实现每个阶段的处理过程。
举例来说,我们可以通过2.2.1中的map来实现信号流图中的映射阶段:
(map square (list 1 2 3 4 5)) ;(1 4 9 16 25)
过滤一个序列,只保留那些满足给定谓词的值:
(define (filter predicate sequence)
(cond ((null? sequence) nil)
((predicate (car sequence))
(cons (car sequence)
(filter predicate
(cdr sequence))))
(else (filter predicate
(cdr sequence)))))
(filter odd? (list 1 2 3 4 5)) ;(1 3 5)
累加:
(define (accumulate op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(accumulate op
initial
(cdr sequence)))))
(accumulate + 0 (list 1 2 3 4 5)) ;15
(accumulate * 1 (list 1 2 3 4 5)) ;120
(accumulate cons nil (list 1 2 3 4 5)) ;(1 2 3 4 5)
那么只剩下一个过程需要实现了,那就是“枚举”!
要枚举一个区间中的数字,我们可以这样做:
(define (enumerate-interval low high)
(if (> low high)
nil
(cons low
(enumerate-interval
(+ low 1)
high))))
(enumerate-interval 2 7) ;(2 3 4 5 6 7)
要枚举一棵树的叶子,我们可以这样做:
(define (enumerate-tree tree)
(cond ((null? tree) nil)
((not (pair? tree)) (list tree))
(else (append
(enumerate-tree (car tree))
(enumerate-tree (cdr tree))))))
(enumerate-tree (list 1 (list 2 (list 3 4)) 5)) ;(1 2 3 4 5)
现在我们就可以以数据流图中的结构那样重写sum-odd-squares和even-fibs了。
(define (sum-odd-squares tree)
(accumulate
+
0
(map square
(filter odd?
(enumerate-tree tree)))))
(define (even-fibs n)
(accumulate
cons
nil
(filter even?
(map fib
(enumerate-interval 0 n)))))
用序列操作来组织程序的好处在于,它帮助我们设计了一个模块化的程序。也就是说,通过组合相对独立的单元来构造程序。
在实际的应用中,设计者们也应经常使用这些操作来构建系统。
(define
(salary-of-highest-paid-programmer
records)
(accumulate
max
0
(map salary
(filter programmer? records))))
符号数据
到目前为止,我们所用的复合数据类型最终还是由数字构成的。
本节我们通过引入将任意符号作为数据的能力来拓展语言的表达能力。
引用
如果我们可以用符号来构造复合数据,那么我们就可以有这样的列表:
(a b c d)
(23 45 17)
((Norah 12)
(Molly 9)
(Anna 7)
(Lauren 6)
(Charlotte 4))
列表可以包含的符号看起来就像我们语言中的表达式:
(* (+ 23 45) (+ x 9))
(define (fact n)
(if (= n 1)
1
(* n (fact (- n 1)))))
为了能够管理符号,我们需要我们语言中的一个新元素: 引用数据对象的能力。
设想我们想要构造列表(a b),我们无法通过(list a b)实现,因为这个表达式构造的是包含a和b的值的列表而不是符号本身。
这个问题在自然语言中也很常见,单词和语句可以当做语义实体或是字符串(语法实体)。
自然语言中常用的办法是用一个引号来指示一个单词或句子是否应该被当做字符串。
For instance, the first letter of “John” is clearly “J.”
If we tell somebody “say your name aloud,” we expect to hear that person’s name.
However, if we tell somebody “say ‘your name’ aloud,” we expect to hear the words “your name.”
这里我们被迫用嵌套的引号来描述别人可能要说什么。
接下来我们也是用这种方式来指示列表和符号应该被当做数据对象,而不是被当做应该被求值的表达式。
不过我们的引用方式和自然语言中的有一点不同,我们在要引用的数据对象前放一个单引号(’)。
现在我们可以区分符号和值了:
(define a 1)
(define b 2)
(list a b) ;(1 2)
(list 'a 'b) ;(a b)
(list 'a b) ;(a 2)
引用也使得我们得以以传统的列表的打印方式来输入复合对象:
(car '(a b c)) ;a
(cdr '(a b c)) ;(b c)
那么我们现在可以用’()来表示空列表,也可以因此放弃使用nil变量了。
eq?过程接收两个符号作为参数,并检查他们是否相同。
通过eq?,我们可以实现一个很有用的过程叫做memq。它接收两个参数,一个符号和一个序列。如果序列中不存在一致的符号,则其返回false。其他情况则返回一个以该符号第一次出现开始的子序列。
(define (memq item x)
(cond ((null? x) false)
((eq? item (car x)) x)
(else (memq item (cdr x)))))
(memq 'apple '(pear banana prune)) ;#f
(memq 'apple '(x (apple sauce) y apple pear)) ;(apple pear)
用例-表示Set
之前为有理数选择的表示方式是很直观的,但表示集合时,这个选择就很多了,而这些实现相比又有很大的不同。
简单来说,Set就是一个由各不相同的对象组成的集合。
如果要下一个更精确的定义,我们可以借用数据抽象的方法。也就是我们通过指定能用在set上的操作来定义‘set’。
它们是union-set, intersection-set, element-of-set?和adjoin-set。
- element-of-set? 是一个谓词,判断set中是否含有指定元素。
- adjoin-set 接受一个对象和一个set作为参数,并返回一个包含原来set和新对象的set。
- union-set 计算两个set的并集
- intersection-set 计算两个set的交集
从数据抽象的角度来说,我们可以自由的设计表示方式来实现与上述解释相符的操作。
set作为无序序列
一种表示set的方式就是用序列表示并使得这个列表中不包含出现过一次以上的元素。
如此我们就可以实现element-of-set?了,这里用equal?而不是eq?来比较,所以set的元素不一定得是符号(eq?是比较符号的)。
(define (element-of-set? x set) (cond ((null? set) false) ((equal? x (car set)) true) (else (element-of-set? x (cdr set)))))实现adjoin-set,如果对象已经在set中,就直接返回set。如若不然,我们通过cons将对象添加到表示set的序列中。
(define (adjoin-set x set) (if (element-of-set? x set) set (cons x set)))我们可以用递归来实现intersection-set。如果我们知道如何产生set2和(cdr set1)的交集,那么我们只要决定是否包含(car set1)就可以了。
如何决定是否保留呢?这得看(car set1)是否也在set2中了。
(define (intersection-set set1 set2) (cond ((or (null? set1) (null? set2)) '()) ((element-of-set? (car set1) set2) (cons (car set1) (intersection-set (cdr set1) set2))) (else (intersection-set (cdr set1) set2))))在设计表达方式的时候,我们需要关注的一个问题就是”效率“。
考虑下我们set操作需要的步骤数是多少?
因为这些操作都要用到element-of-set?,所以这个操作的速度很大程度上影响着整个表达方式的效率。
为了检查一个对象是不是一个set的成员,element-of-set?可能需要扫描整个set(在最差的情况里,对象不在set中)。
因此,如果set中有n个元素,那么element-of-set?最大可能需要n步。因此运算步骤增长的阶为Θ(n)。
相应的,使用了这一过程的adjoin-set,其增长的阶也是Θ(n)。
而对于intersection-set,这一过程对set1中的每一个元素都应用了element-of-set?,所以对应的增长的阶为set1和set2的大小的乘积,对于两个set大小都是n的情况,增长的阶是Θ(n2)。
union-set也是这样。
set作为有序序列
有一种方式可以使我们的set操作更快,那就是去修改表达方式,使得set的元素以升序(逆序也可以啦,这里是方便后面叙述)的方式存在序列中。
那么我们需要一些方法来比较两个对象。
例如,我们可以比较符号的字母顺序,或者我们给每个对象分配一个独一无二的数字,然后就可以通过比较数字来比较元素啦。
为了简化讨论,我们只考虑set中的元素都是数字的情况,因此我们也可以通过>和<来比较元素。
用之前的方式表示set {1,3,6,10},我们可以将元素以任何顺序放在序列中,但是通过我们新的表示方式,只允许(1 3 6 10)这种形式。
将元素有序地排列的一个好处体现在element-of-set?中就是,我们不再需要扫描整个set来检查元素是否在set中。
如果我们查找到一个比我们要找的元素还要大的元素时,我们就可以确定那个元素不在这个set中了。
(define (element-of-set? x set) (cond ((null? set) false) ((= x (car set)) true) ((< x (car set)) false) (else (element-of-set? x (cdr set)))))这个实现节省了多少步计算?
在最差的情况下,我们查找的元素是set中最大的元素,那么这时使用的计算步骤和和之前使用无序序列的情况是一样多的。
在最好的情况下,我们查找的元素接近于set中最小的元素,那么计算会在接近开始点就终止。
我们可以期待平均需要检查set中一半的元素。
因此,平均需要的步骤大约是n/2。其增长的阶依然是Θ(n),不过这相对之前的实现,确实平均给我们节省了n/2的步骤数。
我们在intersection-set中可以得到更显著的速度提升。
因为我们针对set1中每一个元素在set2中做了完全扫描,所以无序列表中这个操作需要Θ(n2)步。
但是在有序表达方式中,我们可以使用一种更加聪明的方法。
从比较初始元素x1和x2开始,如果两者相等,那么向交集中增加一个元素,而交集中剩下的元素则是从两个set的cdr中取。
如果x1小于x2,又因为x2是set2中最小的元素,我们可以马上知道,x1不会在set2中出现,也就不会在交集中出现了。因此set1和set2的交集等同于(cdr set1)和set2的交集。
类似的,如果x2小于x1,那么set1和set2的交集等同于set1和(cdr set2)的交集。
(define (intersection-set set1 set2) (if (or (null? set1) (null? set2)) '() (let ((x1 (car set1)) (x2 (car set2))) (cond ((= x1 x2) (cons x1 (intersection-set (cdr set1) (cdr set2)))) ((< x1 x2) (intersection-set (cdr set1) set2)) ((< x2 x1) (intersection-set set1 (cdr set2)))))))为了估算这个计算过程需要的步骤,观察我们每一步是如何将交集问题规约为求更小的set的交集的–通过移除set1或set2又或者set1和set2中的首个元素。
因此需要的步骤最多为set1和set2的大小之和,而不是无序表示中的两者大小之积。
增长的阶为Θ(n)而不是Θ(n2) —— 就算是相对小的集合来说,这也是很可观的提速了。
set作为二叉树
我们可以通过将set中的元素组织为树的形式来获得更好的性能。
树的每个节点存放set中的一个元素,这一元素叫做节点的数据项,还有一个与其他两个节点(可能为空)的链接。
左链接指向比节点值小的节点,右链接指向比节点值大的节点。
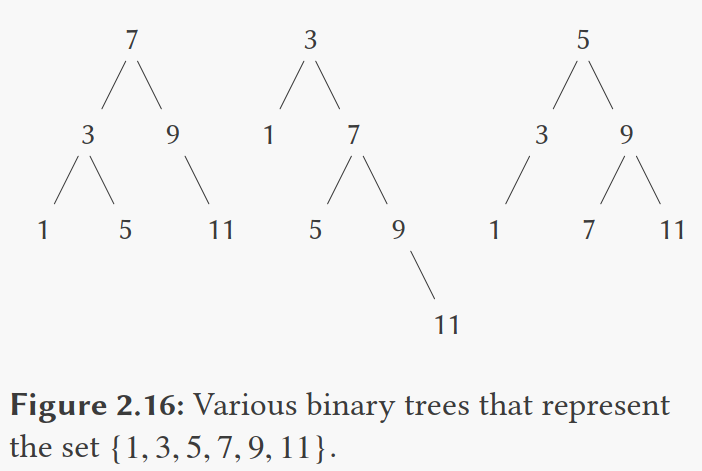
同样的set也可能表示为不同形式的树。
对有效的表示方式的唯一要求是,所有左子树的元素比节点的数据项要小,而所有右子树的元素比节点的数据项要大。
用树来表示好处是: 设想我们需要检查x是否在一个集合中,我们先比较x与根节点的数据项,如果x要更小,则我们知道接下来只需要到左子树中查找,如果x要更大,则接下来只需要到右子树查找。
如果树是”平衡的“,那么每个子树占树的一半大小。
因此,我们每一步都能将在大小为n的树中搜索的问题规约至在大小为n/2的树中搜索的问题。
每一步都把树的大小均分,那么我们可以预期搜索大小为n的树的计算所需步骤的增长的阶为Θ(log{n})。
对于大型的set来说,这将显著提升速度。
我们可以用序列来表示树。每个节点对应一个三元素的列表: 节点中的数据项,左子树和右子树。如果左子树或右子树为一个空列表,则表示没有对应的子树。
(define (entry tree) (car tree)) (define (left-branch tree) (cadr tree)) (define (right-branch tree) (caddr tree)) (define (make-tree entry left right) (list entry left right))现在我们来写相对应的element-of-set?
(define (element-of-set? x set) (cond ((null? set) false) ((= x (entry set)) true) ((< x (entry set)) (element-of-set? x (left-branch set))) ((> x (entry set)) (element-of-set? x (right-branch set)))))将一项数据连接到set中也可以以类似的方法实现,其增长的阶也是Θ(log{n})。
(define (adjoin-set x set) (cond ((null? set) (make-tree x '() '())) ((= x (entry set)) set) ((< x (entry set)) (make-tree (entry set) (adjoin-set x (left-branch set)) (right-branch set))) ((> x (entry set)) (make-tree (entry set) (left-branch set) (adjoin-set x (right-branch set))))))以上关于搜索树可以以对数级别的步骤完成的声称是建立在树是”平衡的“这一假设之上的。
如果我们从空set开始,依次邻接1-7,我们将得到一个高度不平衡的树:
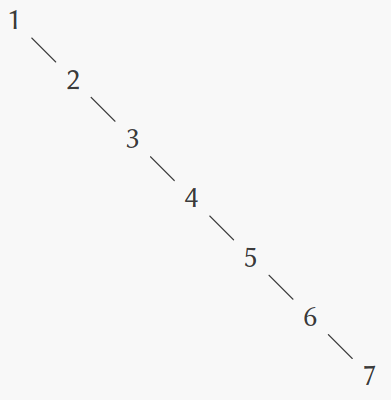
如果树不是”平衡的“,我们必须实现一个方法来将其转化为”平衡的“。然后在数次adjoin-set操作后调用这一转化操作使我们的set保持平衡。
当然也有其他办法可以解决这个问题,其中大多数方法都涉及到设计一个支持在Θ(log{n})步骤中完成搜索和插入的新的数据结构。(例如B树和红黑树)
set与信息检索
我们考察了用表表示set的各种选择,并看到了数据对象表示的选择对使用数据的程序的性能有多大的影响。
另一个关注set的原因就是,这里讨论的技术在涉及到信息检索的应用中一次又一次地出现。
考虑一个包含了大量独立记录的数据库,例如一家公司的人事档案或是账务系统中的事务清单。
数据管理系统一般在访问和修改记录中的数据中花费了大量时间,因此需要一个有效的访问记录的方法。
可以通过标识记录中的一部分为”键“来实现。键可以是任何可以唯一标识记录的东西。对于人事档案,可以用雇员的身份号码。对于账务系统,可以使一个事务编号。
无论键是什么,当我们定义记录的数据结构时,我们应该实现一个键的选择器用来从指定记录中取出键。
现在我们可以将数据库表示为一个记录的集合。
#(define (lookup given-key set-of-records) (cond ((null? set-of-records) false) ((equal? given-key (key (car set-of-records))) (car set-of-records)) (else (lookup given-key (cdr set-of-records)))))当然,除了用无序序列,还有许多更好的方式可以用以表示大型的集合。
能够随机访问记录的信息检索系统中,一般是通过基于树的方法实现的,例如之前讨论的二叉树。
在设计这样的系统的时候,数据抽象的方法论就显得很有帮助了。
设计者可以先用一种简单,直接的表示(如无序序列)来创建一个初始的实现。这个实现虽然不适合最终的系统,但它可以提供一个”quick and dirty“的数据库用以测试系统的其他部分。
之后,数据的表示可以修改得更加成熟。如果数据库是被从抽象的选择器和构造器访问的,那么表示上的修改将不会导致系统剩余部分的修改。
抽象数据的多种表示
(display 'hello)